What’s SUSY all about?

As I discussed in one of my past blog post The Standard Model and Beyond, the Standard Model of particle physics is a Quantum Field Theory that describes the fundamental bulding blocks of nature, and how they behave. It includes the fermions (three pairs of quarks and three pairs of leptons), and the fundamental force carriers, the bosons that bring in the interaction amongst these fields. Now, in order to ensure that the Standard Model Lagrangian in local gauge invariant and renormalizable, these force particles have to be all massless. However, the UA1 and UA2 experiments at CERN’s Super Proton Synchrotron (SPS) in 1983 confirmed the historic discovery of the W and Z bosons having masses of around 80 GeV and 91 GeV respectively. A solution to this was proposed by Peter Higgs and his contemporaries: Gauge bosons acquire masses in a local gauge invariant manner through spontaneous symmetry breaking. There are more ellaborate discussions about this in these papers- Paper 1 ; Paper 2 ; Paper 3 ; and Paper 4. The theory predicted an additional field, the Higgs Field with a corrsponding massive Spin 0 particle called the Higgs Boson. The interaction of fundamental particles with the Higgs Field gave them their mass. The Higgs boson interacts with the gauge bosons, with the fermions, and has cubic and quartic self-interactions (responsible for the mass of the Higgs boson itself). More details about the Theory of Higgs Field can be found in my post The Mystery of Higgs. Although the theory was developed in the ’60s, the confirmation of the Higgs boson came in with ATLAS, and CMS detectors at the Large Hadron Collider, CERN in the year of 2012, completing the last piece of missing puzzle of the Standard Model.

Although the SM has been tested to excellent levels of precision and no experimental observation has invalidated its predictions. However, it fails to answer a lot about the universe around us at its fundamental level both experimentally, as well as theoretically. How can the gravitational interaction be included in the theory? What is the source of the charge-parity violation leading to the matter vs antimatter asymmetry in the Universe? What is the origin and composition of the dark matter in the Universe? What is the origin of the particle quantum numbers? How do neutrinos acquire mass? Is there a group framework to unify all interactions at some grand unified scale? These questions are what leads us to the topic of discussion, The Theory of Supersymmetry. Many theories have been developed to resolve the shortcomings of the Standard Model. Out of many, Supersymmetry (SUSY) is one of the most compelling.

Supersymmetry

The Supersymmetry is the proposed theory of Space-time that relate fermions and bosons. Making the Standard Model Supersymmetric brings in a fermionic superpartner to each boson, and a bosonic superpartner to each fermion, thereby doubling the total number of particles in our model. In addition to this a new parity called the R-parity is introduced, which is defined as R = (-1)^3(B-L)+2S, where B, L, and S are the baryon number, lepton number and spin of the particle respectively. All Standard Model Particle have a R- parity of +1, whereas all their supersymmetric partners have a R-parity of -1.

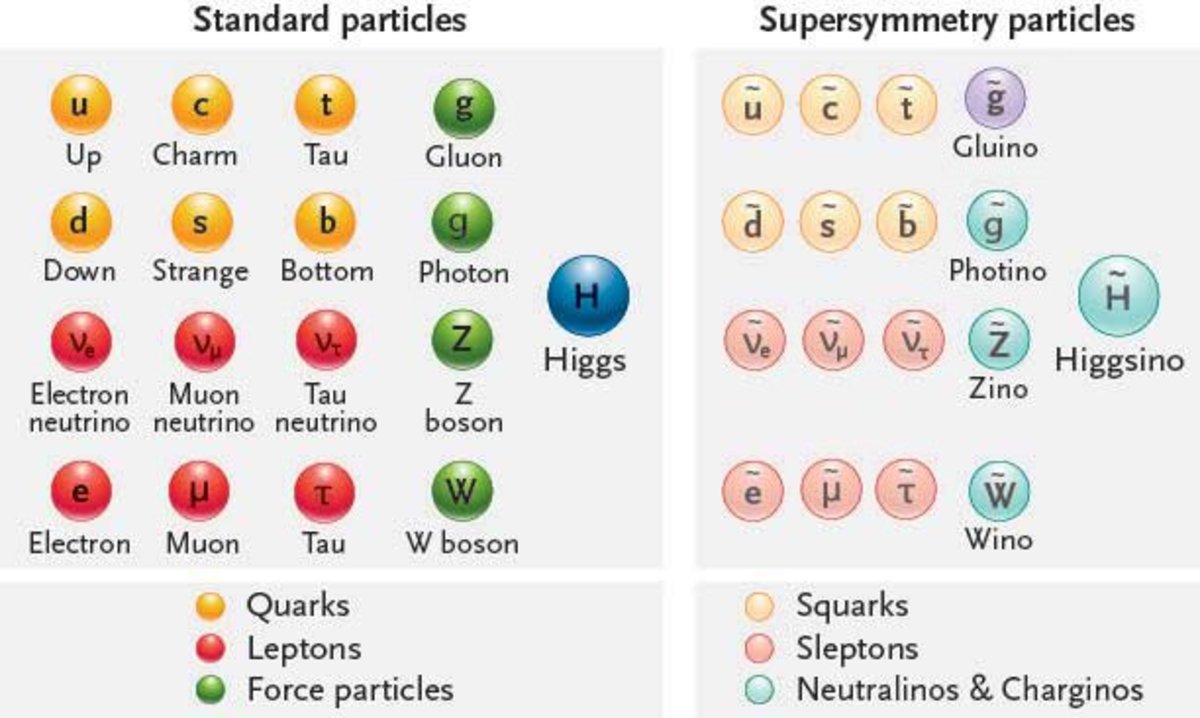
drawing

Developed in the '60s, SUSY has turned out to be an appealing theory in the recent years, as it satisfactorily answers quite many puzzles that SM alone couldn't resolve:

Local Supersymmetric transformations, lead to the introduction of a Spin2 boson, the graviton that mediates the gravitational interactions, along with gravitino, its superpartner. This incorporates General Relativity as a gauge field
In R-parity conserving models the lightest of all supersymmetric particle is satble, and interacts only with weak interactions. This can be an excellent dark matter candidate explaining the extra 27% of invisible matter present in the universe, theorised and estimated via gravitational lensing and galaxy rotation curves.
It allows a Grand Unification of the Electromagnetic, Weak, and the Strong Interactions which otherwise isn't yielded by the Standard Model.

I donot want you to fully understand what each of these points literally mean at this stage. However, I would like you to appreciate that these are just some of the main higlights that makes SUSY a plausible extension of the the Poincare space-time symmetry group, or maybe we can say the Standard Model of Particle Physics. ALthough a proper theoretical understanding of Supersymmetry requires quite of an expertise in Field Theory, however for more advanced and motivated readers, Supersymmetric gauge theories by Baer and Tata, and Basics of supersymmetry with emphasis on gauge theories from the book Advanced Topics in Quantum Field Theory by Shifman is a great starting point.

However, as far as this post is concerned, we are not goig to deal with a lot of theoretical understanding and mathematical structure of supersymmetry, rather try to understand the bare minimum that is required to know and understand the experimental analysis and research going on in the field of High Energy Physics. In the next section, we will deal with the Minimal Supersymmetric Standard Model (MSSM), which is the supersymmetric extension of the SM with the smallest possible number of new fields.

Minimal Supersymmetric Standard Model (MSSM)

In the MSSM for every chiral fermion (having 2 helicity states), there exists a scaler complex field (with two degrees of freedom). Together they form the chiral supermultiplet and transform into each other under supersymmetric transformtion. The scalar quarks are called squarks and the scalar leptons are called sleptons. They are generaly denoted by a tilde over the symbol of their corresponding standard model partner. Eg: A selectron, the superpartner of an electron is denoted by $\tilde{e}$ . The Standard model Higgs doublet gets extended into a chiral supermultiplet by additional spin-1/2 Higgsinos. But after the electroweak symmetry breaking it can give mass only to the up-type quarks. Another Higgs supermultiplet needs to be introduced to give mass to the down-type quarks and charged leptons. The gauge fields of the SM are extended by spin-1/2 fermionic fields called collectively gauginos to form vector supermultiplets. The superpartners of the gluons are called gluinos and the superpartners of the W and B bosons are the winos and bino, respectively.

Wait! What is a B- boson? We didn't see that in the Standard Model. Well, we'll get into more details about that later in some other blog post, just for the time being know that there are four electroweak (unification of the electromagnetic and weak interactions) gauge fields in the standard model- the three weak isospin fields $W_{1}$ , $W_{2}$ , $W_{3}$ and a weak hypercharge field $B$ . The phenomena of electroweak symmetry breaking leads to $W_{3}$ and $B$ to coalesce into two different physical bosons with different masses- the $Z^{0}$ , and the $\gamma$ . The $W_{1}$ , and $W_{2}$ on the other hand form the massive $W^{\pm}$ bosons.

After this short detour, lets get back to our discussion. This completes all the particles in our MSSM. Actually this is not quite an end to what I want talk about SUSY, since there are some more stuff that are essential in order to get started with the basics of Supersymmetry. Experiments tell us SUSY cannot be an exact symmetry. What it means is supersymmetry has to be a spontaneously broken symmetry at some higher scale, whose effect at the electroweak scale is the presence of mass terms of these supersymmetric particles, hence they haven't been observed as they are a lot heavier than the standard model particles. Without assumptions on the supersymmetry breaking mechanism, these mass terms can be considered as independent parameters.

The spontaneous electroweak symmetry breaking leads to significant mixing of the superpartners of the third generation fermions (the third generation squarks and sleptons). Now a valid question to ask is why just the third generation? It is due to their large Yukawa coupling. Lets push this discussion for some other time and focus on where we are going. Due to the electroweak symmetry breaking the bino, winos and higgsinos mix to form two charged mass-ordered states called the charginos $\tilde{\chi}^{\pm}_{i}$ , and four neutral mass-ordered states called neutralinos $\tilde{\chi}^{0}_{j}$ . They are collectively called the electroweakinos. My main motivation for describing all these was to emphasise that as massive , stable particles, the lightest of the four neutralinos is an excellent dark matter candidate. The lightest neutralino of roughly 10 GeV to 10 TeV is what we popularly know as the WIMP (Weakly Interacting Massive Particle) dark matter candidate. So, now we atleast have a rough idea about how MSSM deals with dark matter problem of our standard model. Focussing on other problems that MSSM resolves, such as the hierarchy problem, is a bit challenging at this stage.

We can go on and on discussing deeper and mathematically more intricate stuff about SUSY, however I want to keep the initial blog posts easy and understandable to everyone who has bare minimum knowledge of Particle Physics and want to get a bird's eye view of what 'High Energy Physics' lookas like in order to get started. We can pull off this discussion at a much deeper level of mathematical understanding in a future post :)